ACTIVE CONTOUR UNET WITH TRANSFER LEARNING FOR MEDICAL IMAGE SEGMENTATION
ABSTRACT Segmentation is of the most challenging tasks in medical image analysis and widely developed for many clinical applications. Deep learning-based approaches have achieved impressive performance in semantic segmentation but are limited to pixel-wise settings with imbalanced-class data and weak boundary problems. We tackle those limitations by developing a new two-branch deep network architecture which takes both higher and lower level feature into account. The first branch extracts higher level feature as region information by a common encoder-decoder network structure. The second branch focuses on lower level feature as support information around boundary. Our key contribution is the second branch which treats the object contour as a hyperplane and all data inside a narrow band as supportive information for the position and orientation of the hyperplane. The proposed NB-AC loss is able to incorporate into both 2D and 3D deep network architectures and has been evaluated on challenging medical image datasets (DRIVE, iSeg17, MRBrainS13, MRBrainS18 and Brats18). The experimental results have shown that the proposed NB-AC loss outperforms other mainstream loss functions: Cross Entropy, Dice, Focal on two common segmentation frameworks Unet and FCN. Our 3D network which is built upon the proposed NB-AC loss and 3DUnet framework archives the state-of-the-art results on multiple volumetric datasets. Keywords: Deep Learning, Medical, Segmentation, Imbalanced-Class, Weak BoundaryINTRODUCTION
Medical image segmentation has been widely studied and developed for refinement of clinical analysis and applications [1, 2, 3, 4, 5]. Most deep learning (DL)-based segmentation networks have made use of common loss functions. These losses are based on summations over the segmentation regions ignoring the geometrical information (edge/boundary) and are pixel-wise sensitivity and unfavorable to small structures limited to imbalanced-class data and weak boundary problems. However, (i) boundary information plays a significant role in many medical analysis; (ii) Medical images with weak boundaries are much more challenging to segment due to low intensity contrast, and intensity inhomogeneity; (iii) Also, imbalanced class data is naturally existing (Fig. 1 and Fig.2). Fig.2(a) illustrates the imbalanced-class problem through the statistical class distribution of four different datasets. Fig.2(b) shows statistical values of Mean/Std/Median of pixel intensity in individual class. Strong correlation between classes makes distinguishing classes more challenging especially at the boundary (Fig.1).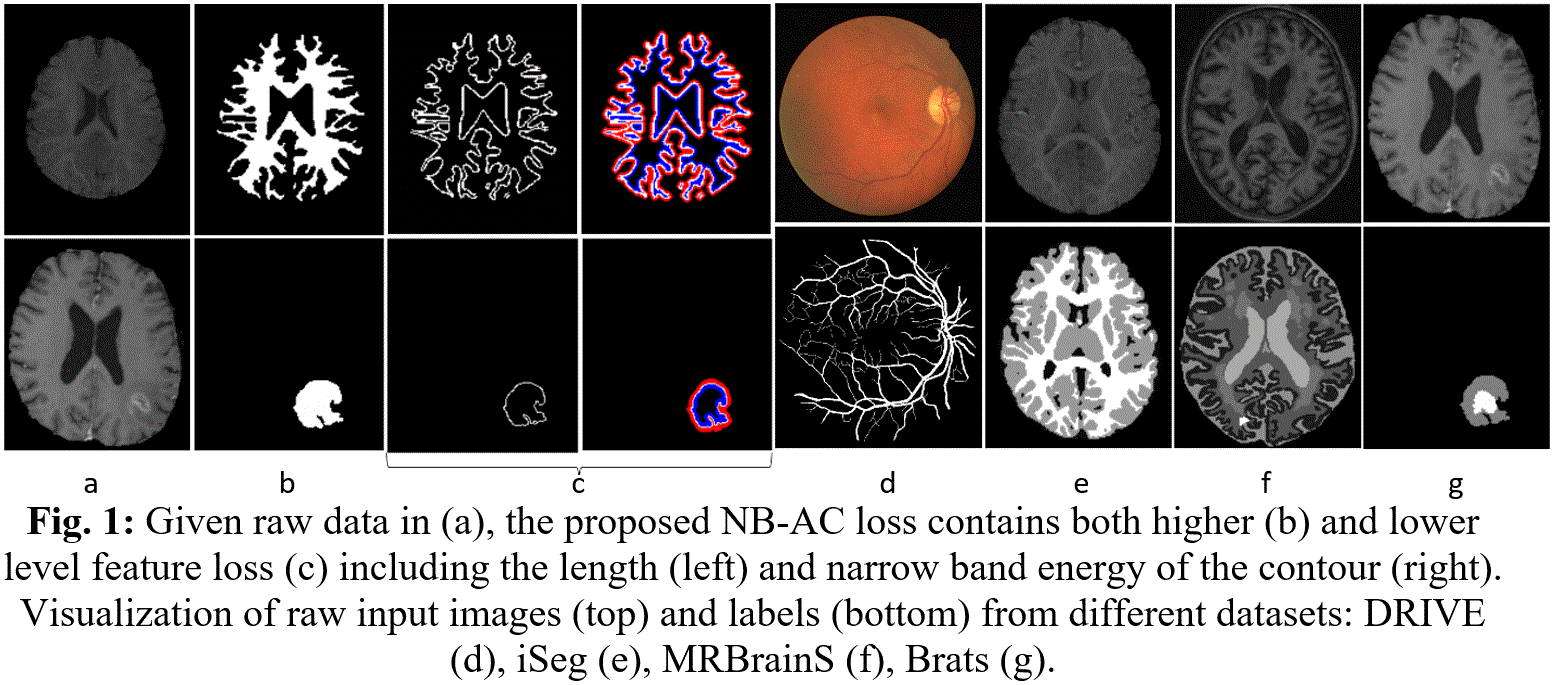
Over the past few years, many efforts [8, 9, 10] have been proposed to segment weak boundary objects. Among which, active contour (AC) methods are powerful with the ability to adapt their geometry and incorporate prior knowledge about the structure of interest. For instance, Level Set (LS) [11], an implementation of AC using energy functional minimization [12] has been proven to overcome the limitations of uniquely gradient-based models, especially with datasets suffering from noise and low contrast. Recently, [1] utilized LS [11] into DL framework for medical images segmentation with the energy terms are computed using constants mean values for inside and outside contour on the entire image domain. Our proposed network makes use of LS as an attention gate on narrow band around the contour and the mean values of inside and outside contour are computed with the deep feature map. Besides, the unbalanced data problem in medical image segmentation has been getting serious attention [13]. One solution is a boundary loss, a distance metric on the space of contours [13] implemented between single pixel on the contour which is time consuming. Hence, our proposed NB-AC focuses on the contour length and narrow band energy, treating the object contour as a hyperplane and all data inside a narrow band supports information for the position and orientation of the hyperplane.
To address the above problems, we make use of the advantages of LS [11], propose a two-branch deep network explicitly taking into account both higher (object region via a classical CNN, an encoder-decoder network structure) and lower level features (object shape with narrow band around the contour). The proposed loss for our NB-AC attention model contains two fitting terms: (i) the length of the contour; (ii) the narrow band energy formed by homogeneity criterion in both inner and outer band neighboring the evolving curve or surface (Fig. 1). The higher level feature is connected to the lower level feature through our proposed transitional gates and both are designed in an end-to-end architecture processed simultaneously. Thus, our loss function pays attention to both region information and support information at the boundary’s narrow band. We consider the object contour as a hyperplane whereas information in the inner and outer bands as a supporter influencing the position and direction of the hyperplane. The keys to our architecture are: (1) Proposed NB-AC attention model extracts edge, makes use of the narrow band principle under an AC energy minimization, which has been proven to be efficient in the LS evolution and for the weak boundary object segmentation [11, 14]. (2) The NB-AC attention model focuses on a subset of supportive pixels within the narrow band as an under-sampling approach removing samples from the majority class to compensate for imbalanced classes distribution. (3) Propose a new type of transitional gate that allows the higher level feature to interact with the lower one in an end-to-end framework. To the best of our knowledge, this is of the first works taking both the imbalanced-class data and weak boundary problem into account by integrating the length of the boundary and minimizing the energy of the inner and outer bands around the curve or surface. We evaluate with both 2D and 3D networks on various challenging datasets: DRIVE [15] - retinal vessel, iSeg [16] - infant brain, MRBrainS [17] - adult brain, Brats [18] - brain tumor segmentation.
METHOD
Our proposed network contains two branches (Fig.3). The first branch focuses on higher level feature presentation (i.e region) whereas the second branch targets at lower level feature representation (i.e. contour). The first branch is built upon region information whereas the second is built upon narrow band energy and the length of the contour.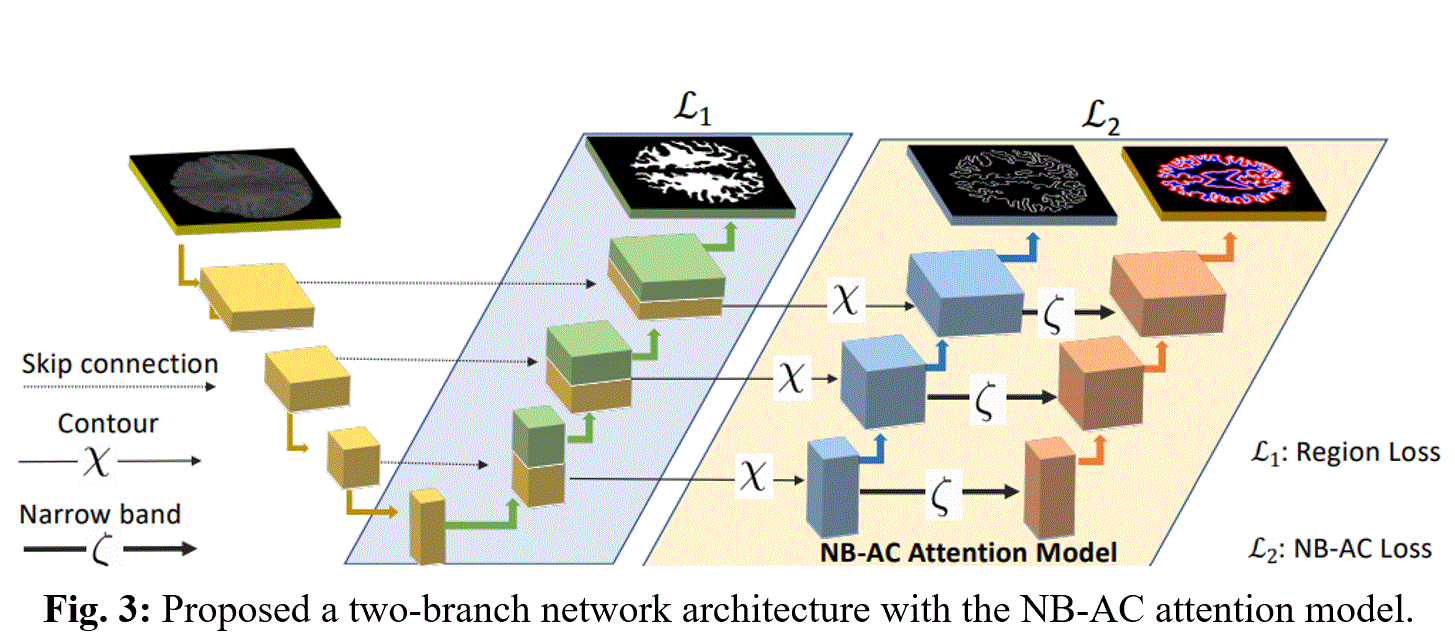
The first branch of the network is a standard segmentation CNN which can utilize any encoder-decoder network. Both Unet and FCN are chosen as the network backbones in our experiments. For a region segmentation of K classes, the first branch outputs the categorical distribution and the loss is: $\sc{L}_1 = - ∑↙{c=1}↖k y^c_o log p^c_o$ where $y^c_o$ is binary indicator (0 or 1) if class label 'c' is the correct classification for observation 'o' and $p^c_o$ is predicted probability observation 'o' is of class 'c'. Then a transition gate will transfer information from the first to the second branch. Let denote the output feature representation of the first branch as $F_\sc{H}$. The output from NB-AC attention model in the second branch is denoted as $F^C_{\sc{L}}$ and $F^N_{\sc{L}}$ (contour and narrow band feature map). The contour feature map $F_\sc{L}^C$ is obtained by applying edge extraction operator χ on the higher level feature map $F_\sc{H}$ and the narrow band feature map $F_\sc{L}^N$ is obtained by applying parallel curves operator ζ on $F_\sc{L}^C$. In our experiments, χ and ζ are chosen as the gradient operator and the dilation operator, respectively.
For the second branch, instead of dealing with the entire domains Ω defined by the evolving curve, we only consider the narrow band: inner band $B_{in}$ and outer band $B_{out}$ from two sides of the curve $C$ (note: $C$ is presented by $Φ = 0$, with $Φ$ is the signed distance map from every pixel on the entire image to the given contour). Our NB-AC loss of the second branch is: $\sc{L}_2=μ∫_w|Length(Φ)|dxdy+λ_1 ∫_{B_{in}}|p-b_{in}|^2 dxdy+λ_2 ∫_{B_{out}}|p-b_{out}|^2 dxdy$. Hence, the whole objective function for this Unet-like with NB-AC attention model is as follow: $\sc{L}_{NB-AC}=λ_1 \sc{L}_1+λ_2 \sc{L}_2$, where $λ_1$ and $λ_2$ are parameters controlling weights between losses.
EXPERIMENTS
Dataset. We use four common medical datasets including 2D and 3D images in our experiments as follows. DRIVE: Digital Retinal Images for Vessel Extraction [15] contains 40 colored fundus photographs, with size of 565×584, divided into 20 images for training and validation, 20 images for testing. To reduce the overfitting problem and the calculation complexity, our model is trained on 19,000 small patches sized 224×224 randomly extracted from 20 training images. iSeg: [16] consists of 10 subjects for training and 13 subjects for testing. Each subject includes T1 and T2 images with size of 144×192×256, and image resolution of 1×1×1 mm3. MRBrainS: The MRBrainS13 dataset contains 6 subjects for training and validation and 15 subjects for testing. The MRBrainS18 [17] contains 7 subjects for training and validation and 23 subjects for testing. For each subject, three are T1-weighted, T1-weighted inversion recovery and T2-FLAIR with image size of 48×240×240. Brats: [18] contains 210 HGG scans and 75 LGG scans. For each scan, there are 4 available modalities. Each image is registered to a common space, sampled to an isotropic 1×1×1 mm3 resolution with dimension of 240×240×155. Experiment Setting. On 2D images, to train our NB-AC loss on 2D networks (FCN, UNet) we define the input as N × C × H × W, where N is the batch size, C is the number of input modalities and H, W are height, width of 2D image. Corresponding to DRIVE, iSeg17, MRBrainS18 and Brats18, we choose the input as 4×3×224×224, 4×2×224×224, 4×3×224×224 and 4 × 4 × 224 × 224, respectively. We employed the Adam optimizer, with a learning rate of 1e-2 with weight decay 1e-4. On 3D volumes, our 3D architecture is built upon 3D-Unet [4] and the input is defined as N × C × H × W × D, where N is batch size, C is the number of input modalities and H, W, D are height, width and depth of volume patch on sagittal, coronal, and axial planes. Corresponding to Brats18, MRBrainS13 and iSeg17, we choose the input as 1 × 4 × 96 × 96 × 96, 1×3×96×96×48, and 2×2×96×96×96. We implemented our network using PyTorch 1.3.0 and our model is trained until convergence by using the ADAM optimizer. We employed the Adam optimizer, with a learning rate of 2e-4. Our 3D Unet makes use of instance normalization [38] and Leaky reLU. The experiments are conducted using an Intel CPU, and RTX GPU.RESULTS
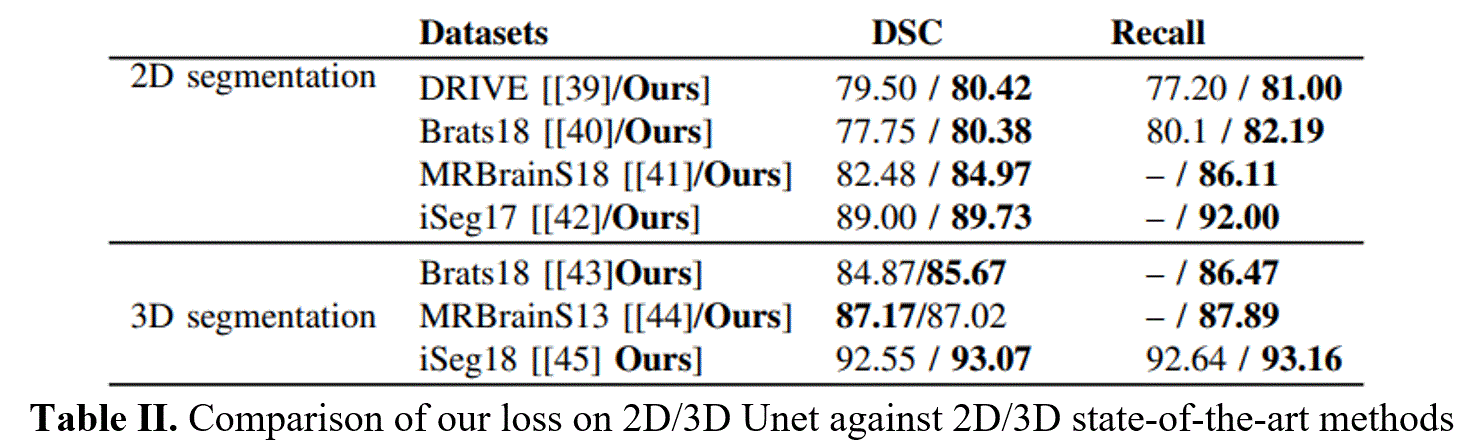
For quantitative assessment of the segmentation, the proposed model is evaluated on different metrics, e.g. Dice score (DSC), Intersection over Union (IoU), Sensitivity (or Recall), Precision (Pre). The performance of our proposed NB-AC loss is evaluated on both FCN [35] and Unet [3] architectures for 2D input and 3DUnet [4] for 3D input. The comparisons between our proposed loss and other common loss functions: CE, Dice, Focal on challenging datasets DRIVE, MRBrainS18, Brats18 and iSeg17 are given in Tables I. Table II shows the comparison against other state-of-the-art methods on three volumetric datasets. Our performance is quite compatible with [44] on MRBrainS13 while it outperforms [43] and [45] on BratS18 and iSeg17 with similar network architecture setting up. For the qualitative results and the topology view comparing the segmented mask example of our loss with other losses, please check further on our either our website, or paper, or project report.
It is clear that the proposed NB-AC loss function outperforms the other common losses under both UNet and FCN frameworks. Take DSC metric on CE loss as an instance, our loss gains 3.97%, 1.36%, 1.39%, 1.0% on DRIVE, MRBrainS18, Brats18, iSeg17 respectively using Unet framework and it gains 0.53%, 1.65%, 0.98%, 0.82% on DRIVE, MRBrainS18, Brats18, iSeg17 respectively using FCN framework.